In this chapter we will show how to write expressions that both involve indexed objects, and which evaluate to indexed objects. It was intended from the outset in the design of REDTEN that the user be able to write tensor expressions in a convenient form, and have them displayed in as close to publication form as was practical.
Whenever the user enters an indexed object with a pattern index (an index in which at least one element is an identifier and not an integer) the indexed object is returned unevaluated (unless the intrinsic symmetries of the object allow an immediate simplification to zero). This has already been seen in the previous chapter, where the concept of an indexed object reference was demonstrated. Now we shall use this to build expressions that can then be used to create new indexed objects.
An ``indexed expression'' consists of the algebraic combination of indexed objects such that the indices involved obey the rules set out below. An indexed expression is a normal REDUCE expression and can be assigned to REDUCE variables, however, if this is done there is no checking of the index structure or other evaluation except for the usual canonicaliztion of indices until the expression is used in an ``indexed assignment''.
An indexed expression can be as simple as
#: r[a,b];or as complicated as need be, given certain rules about indices and the combinations that are valid. In any indexed expression there will be some index elements that are non-integer (otherwise each indexed object reference can be immediately evaluated and a simple algebraic expression results). The labels used for each of these index-elements are arbitrary except for the following restrictions:
The net index structure of the expression, obtained by eliminating the
contractions and fixed indices, will be the same as that of the object
to which the expression will eventually be assigned. Ideally, this
object would be created by the user before the assignment takes place,
so that proper checking of the index structure of the expression
relative to that expected in the output object can be done. The user
can also avoid declaring the object, in which case the system will
prompt as soon as an index is placed on it, or the user can make a
``bare'' declaration (see page 
), and the system will
determine the net index structure of the expression and place the
indextype parameter on the object. This is not recommended.
The net symmetries of the expression are in general very difficult to determine by a simple algorithm, thus it is up to the user to correctly place these on the output object. Failing to do so can result in very long run times for some expressions, since the system uses the output objects' symmetries to generate the indices it uses to perform the evaluation.
Continuing with the Robertson-Walker metric example from the last chapter, we can now construct the two kinds of Christoffel symbols from the metric tensor. In tensor notation these are defined by:
where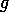 
is the metric tensor. Unfortunately, REDTEN does not
have quite the flexibility of input for the user to use this exact
formalism, so we must resort to making these rank-3 objects with, for
example, the names hc1 and hc2 respectively. In actual
fact, neither of the Christoffel symbols is a tensor, but in the GR
package of REDTEN they are declared as such (with the generic names
c1 and c2), since certain combinations of these objects
are tensors.
It can be seen that the first Christoffel symbol is symmetric in its
first two indices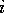 
and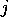 
, while the second Christoffel symbol is
symmetric in its second and third indices, again 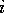and 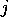, taking
the upper index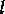 
to be the first. We can then declare these objects,
giving them the proper index structure and symmetries:
#: mkobj ('hc1, '(-1 -1 -1), '((1 1 2)), '(), 'christoffel1);
hc1
a b c
#: mkobj ('hc2, '(1 -1 -1), '((1 2 3)), '(), 'christoffel2);
a
hc2
b c
The Christoffel symbols can be evaluated by:
#: hc1[i,j,k] == (h[i,k,|j] + h[j,k,|i] - h[i,j,|k])/2;
- h + h + h
i j |k i k |j j k |i
hc1 = -----------------------------------
i j k 2
hc1
i j k
#: hc2[l,i,j] == h[@l,@k]*hc1[i,j,k];
l k l
hc2 = h hc1
i j i j k
l
hc2
i j
#: hc1[0,1,1];
- rt rt
t
We first observe that indexed assignments are done using the same == operator that was used to write individual components to indexed
objects, since that operation is a simple form of indexed assignment.
Immediately after the input line has been parsed and depending on the
setting of the switch rewrite the system will ``pretty-print''
the expression to show the user the index structure of the left and
right hand sides. If these do not match, an error message will be
forthcoming.
The system then begins the process of parsing the expression and evaluating each component for the left hand object. If the switch showindices is on, each components index is displayed on the screen as the assignment proceeds. This is useful for complicated objects, where the time to accomplish the assignment may be several minutes and it is desired to monitor the progress of the calculation. The proper display of these indices depends on the correct setting of the variable upcursor, see Appendix F for more information. A related switch is peek which also shows if the current component evaluates to zero or non-zero.
The expression for hc1 involves the ordinary differentiation operator |; when this is encountered the system will create a new object to store the derivatives for future reference. This is described more fully in §4.1. In the calculation of hc2 it will be observed that the shift operator @ has been used on the metric indices. In general, when an indexed object reference is parsed, the system checks for these operators, and, if the corresponding shifted object exists, the reference is rewritten in terms of this object directly. Thus, typing h[@a,@b] is equivalent to typing h_inv[a,b], since the inverse object already exists. If it did not, the operations would be held pending an indexed assignment, and at that time the shift() function would be called to construct the new object. That is, the system does as much simplifcation as it can on the expression as initially entered, but waits until it is involved in an indexed assignment to undertake any time-consuming calculations. The expression for hc2 also contains a contraction representing the summation over the index k. It is here that the diagonal symmetry of the metric can be used effectively, since the summation in this case reduces to a single term.
It will also be observed that the indexed objects in the first of these calculations are involved in an algebraic expression (a quotient). This is a very simple case of a more general property of indexed expressions in REDTEN: an indexed object can be an argument to an algebraic function; the components of the indexed object are evaluated in the context of the function as the indexed expression is evaluated. For example,
#: k[a,b]==sub(s=1, h[a,b])$ #: l[a,b]==df(h[a,b],om)$
With the Christoffel symbols in hand, we can now proceed to evaluate the Riemann curvature tensor, which is defined in terms of the Christoffel symbols by:
It can be shown from symmetry considerations that there are only 21
independent components of the Riemann tensor in a four-dimensional
space-time, rather than the 256 components there appear to
be
. The Riemann tensor is anti-symmetric in the first and
second indices, anti-symmetric in the third and fourth indices, and
symmetric in blocks of two indices starting at the first and third. In
REDTEN notation, this symmetry list is written as '((-1 1 2)
(-1 3 4) (2 1 3)) and the Riemann tensor hR can be made with
the command:
#: mkobj ('hR, '(-1 -1 -1 -1), '((-1 1 2) (-1 3 4) (2 1 3)), '(),
'riemann);
hR
a b c d
Recall that the name R is declared generic in REDTEN and
should not be used to create a Riemann tensor (the name R is
however closely related to the Riemann tensors created with the GR
package).
The assignment to the Riemann tensor is made as follows:
#: hR[h,i,j,k] == hc1[i,k,h,|j]-hc1[i,j,h,|k]+hc2[l,i,j]*hc1[h,k,l]
-hc2[l,i,k]*hc1[h,j,l];
l l
hR = - hc1 hc2 + hc1 hc2
h i j k h j l i k h k l i j
- hc1 + hc1
i j h |k i k h |j
hR
h i j k
If the user examines this object it will be seen that there are only 6
non-zero components. On a reasonably fast computer (eg. a 25Mhz 386
or a SUN) this calculation takes only a few seconds for this metric;
for more complicated metrics it will of course take longer.
The next objects to create are the Ricci tensor and the associated Ricci scalar (also called the scalar curvature). These are defined by
The Ricci tensor is symmetric, hence:
#: mkobj('hRic, '(-1 -1), '((1 1 2)), '(), 'ricci);
hRic
a b
is the command to make the object. There are two ways to compute the
components of both the Ricci tensor and the Ricci scalar, in REDTEN
one method is somewhat more efficient than the other. The first method
is to indicate a shift operation with the @ operator, this will
cause the system to create a new object (whose name is derived from
the name of the object being shifted, see §3.1.2 for more
detail). The internal contraction of the object is then done to yield
the output object:
#: hRic[i,j] == hR[@k,i,j,k];
k
hRic = hR
i j i j k
computing hR_b
SHIFT finished.
hRic
i j
A side effect of this method is the creation of hR_b, a Riemann
tensor with the first index raised, and, incidentally, fewer
symmetries than the original Riemann tensor. Thus, it can take
appreciably longer to compute this object since it has many more
components (12 non-zero ones for this metric). Since we probably are
not interested in this object this particular method is not the most
efficient way to compute the Ricci tensor. Instead, we shall write the
metric contraction explicitly, so that the system simply does a
two-index contraction:
#: hRic[i,j] == h[@l,@k]*hR[l,i,j,k];
k l
hRic = - hR h
i j i l j k
hRic
i j
This calculation computes directly the object of interest and proceeds
much more quickly than the first method. Since the contraction
involves all the indices of the metric inverse, it will be read-out
when the expression is processed (before the actual evaluation of
output components begins) yeilding a substantial simplification. It
will also be observed that the expression as echoed by the system is not
identical to that typed in, since the indices have been canonicalized
and, in the case of the Riemann tensor, a sign change was introduced.
We can similarly evaluate the Ricci scalar using the more efficient metric contraction:
#: hRsc == h[@i,@j]*hRic[i,j];
i j
hRsc = hRic h
i j
2
6 (rt rt + rt + k)
t,2 t
-------------------------
2
rt
Note that we did not declare hRsc in advance. The indexed
expression on the right hand side evaluates to a scalar and REDTEN
will accept a REDUCE scalar as the output object in this case.
In fact, the left hand side can either be an indexed object or a
scalar, and the right hand side can be any indexed expression, scalar
expression, or simple scalar.
#: w[a,b] == 99; % write 99 into every component of w w a bThis example is not generally very useful unless perhaps to set every component of an object to zero. Of course, mixed indices may also be used, in order to limit the assignment to a row or column etc. Only if the right hand side is indexed is it necessary for the left-hand side to be similarly indexed. One can always assign an indexed expression to an object of higher rank; the extra indices may be fixed or pattern indices, if the latter, then the expression is assigned to every possible combination of indices. An error will occur if a pattern index-element on the right hand side is unmatched by a similar one on the left.
#: w[a,b] == p[a]; % this is ok w a b #: p[a] == w[a,b]; % this is an error Error: free index element b in w[a,b].The first assignment will replicate p (assumed to have been created and given some values) into the columns of w. The second assignment fails because there is no index element corresponding to b on the left hand side (it is a ``free'' index element). If, however, w were zero (i.e. with no explicit components and also not implicit) then the assignment would proceed, because the expression
w a bis replaced by zero before the index checking is done. If b were replaced by a valid integer then the assignment could again proceed.
As noted above, the index of the output object can be such that only a portion of the object is referenced during the indexed assignment operation. In this case, any components that are not included in the scope of the index remain unchanged; the new components are merged with the old. If the user decides that an indexed assignment applied to an object with previously defined components has been an error, the old value of the object can be recovered by calling restoreobj() immediately.
The function seval() is used to perform the evaluation of an indexed expression that reduces to a scalar, without the need for an indexed assignment using ==. Thus, the dimension of the space-time can be found by
#: seval(h[@a,@b]*h[a,b]);
a b
seval = h h
a b
4
In fact, this function calls the indexed assignment operator and
assigns the result to the name seval.
The left hand side of these scalar expression can also be an indexed scalar, declared by giving mkobj() an empty indextype property (see §2.2.2). In this case the empty index must be attached to the object name.
Another scalar of interest is formed by contracting the Riemann tensor with itself. The Kretschmann scalar is defined by
We can declare it to be an indexed scalar via
#: mkobj('hkrtch, '(), '(), '(), 'kretschmann);
hkrtch
and evaluate it as follows:
#: hkrtch[] == hR[@a,@b,@c,@d]*hR[a,b,c,d];
computing hR_p
shift finished.
2 2 4 2 2
12 (rt rt + rt + 2 rt k + k )
t,2 t t
----------------------------------------
4
rt
In this instance we allowed the system to create the shifted Riemann
tensor hR_p because it has the same symmetries as hR (and
is not too expensive to compute), but the expression could have been
written with the metric inverse explicitly. Note that forgetting the
empty index on hkrtch is likely to lead to a syntax error. In
order to examine the value of hkrtch it is also necessary to add
the expty index, the name alone has itself as its value.
The remaining objects of interest for the RW metric are the Einstein tensor and the Weyl curvature tensor, defined by:
These object are closely related to the Ricci tensor and the Riemann tensor, respectively, with the same index structure and symmetries and can be created in the following way using the extended mkobj() syntax described in §2.2.2 and §2.2.3:
#: mkobj('hG,'hRic,'hRic, '(), 'einstein);
hG
a b
#: mkobj ('hC, 'hR, 'hR, '(), 'weyl);
hC
a b c d
The evaluation of these objects is straightforward (some of the
constants below depend on the dimension of the space; here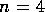 
):
#: hG[i,j] == hRic[i,j]-hRsc*h[i,j]/2;
hG =
i j
2 2
- 3 rt h rt - 3 rt h - 3 h k + hRic rt
t,2 i j t i j i j i j
---------------------------------------------------------------
2
rt
hG
i j
#: hC[h,i,j,k] == hR[h,i,j,k]+(h[h,j]*hRic[i,k]+h[i,k]*hRic[h,j]
-h[i,j]*hRic[h,k]-h[h,k]*hRic[i,j])/2+hRsc/6*(h[h,k]*h[i,j]
-h[h,j]*h[i,k]);
<lots of output>
hC
h i j k
It will be observed that in the expression for the Weyl tensor the
name h is used both for an index and as the metric. Ordinarily
there is no conflict between a name used in an index and the same name
used for any other indexed object or algebraic variable, unless the
switch evalindex is on (qv).
If the contents of the Weyl tensor are examined, it will be found that
there are no explicit values, as is to be expected since the RW metric
is conformally flat.